Class 10 Electricity Important Questions : Solutions
Important Questions Notes Previous Years QuestionsElectricity Important Questions : Solutions
- The potential difference between the terminals of an electric heater is 60 V when it draws a current of 4 A from the source. What current will the heater draw if the potential difference is increased to 120 V.
Sol:
Here, V = 60 V and I = 4 A
Using, R = V/I = 60/4 = 15 Ω
Now, V = 120 V
So, I = V/R = 120/15 = 8 A - The V-I graph of three resistors is shown below. Which resistor has maximum resistance?

Sol:
Resistor R3 has maximum resistance. - An electric iron is marked 400 W and 220 V. What is the resistance when iron is hot? How long could it be used for ₹3 of electrical energy that costs 15 paise per unit.
Sol:
Given, P = 400 W and V = 220 V
Using, P = V²/R
⇒ R = V²/P = 220²/400 = 121 Ω
So, resistance when iron is hot = 121 Ω
Now, rate of electrical energy = 15 paise per unit
and total money = ₹3 = 300 paise
So, electrical energy consumed, E = 300/15 = 20 unit = 20 kWh = 20000 Wh
Using, E = P × t
⇒ t = E/P = 20000/400 = 50 h
So, It can be used for 50 hours. - A 20 cm long uniform wire of resistance 5 Ω is stretched to a uniform wire of 40 cm length. What will be the resistance of new wire?
Sol:
length = l = 20 cm
Area of cross-section = A
Resistance = R = ρl/A = 5 Ω
New length = l’ = 40 cm = 2l
New area of cross-section = A’
When the wire is stretched, its volume remains the same.
So, A’ × l’ = A × l
⇒ A’ × 40 = A × 20
⇒ A’ = A/2
New resistance
= R’
= ρl’/A’
= ρ(2l)/(A/2)
= 4ρl/A
= 4R = 4 × 5 = 20 Ω
Therefore, resistance of the new wire is 20 Ω. - If R1 and R2 are the resistances of filaments of a 400 W and a 200 W lamp, designed to operate on the same voltage, then find the relationship between R1 and R2.
Sol:
For R1, P1 = 400 W
For R2, P2 = 200 W
Using, P = V²/R
(V1)2 = P1 x R1 = 400R1
and (V2)2 = P2 x R2 = 200R2
Since, both filaments operate on the same voltage.
So, (V1)2 = (V2)2
⇒ 400R1 = 200R2
⇒ 2R1 = R2 - .
- State Ohm’s law and write its expression.
Sol:
According to Ohm’s law, at constant temperature, the potential difference across the ends of a conductor is directly proportional to the amount of current flowing through it.
Mathematically,
V ∝ I
V = IR where, R is constant of proportionality & is known as resistance. - Draw a circuit diagram to verify Ohm’s law.
Sol: Circuit diagram for the verification of Ohm’s law: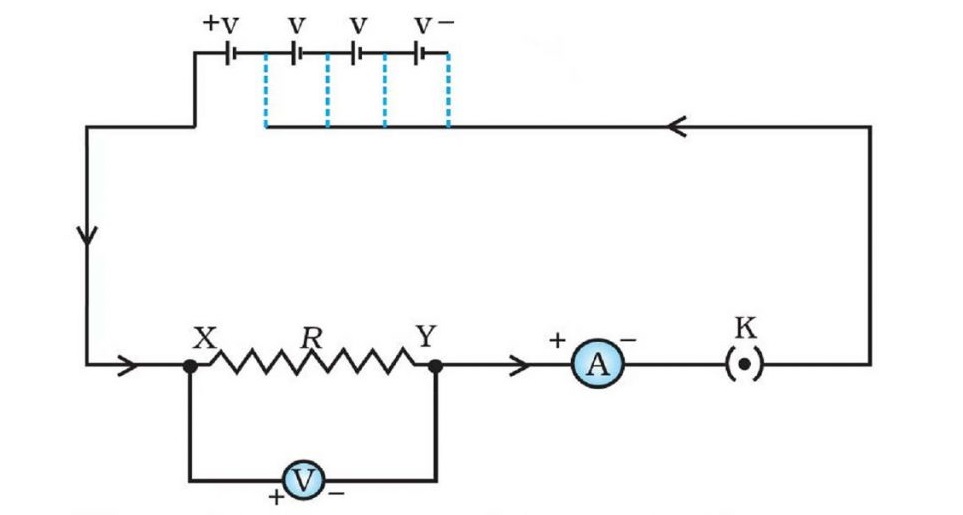
- State Ohm’s law and write its expression.
- The rating of bulb B1 is 60 V, 12 W & bulb B2 is 100 V, 100 W. Find the maximum emf of the battery so that all bulbs remain safe.

Sol:
For B1,
V1 = 60 V, P1 = 120 W
R1 = V1²/P1 = 60²/120 = 300 Ω
For B2,
V2 = 100 V, P2 = 100 W
R2 = V2²/P2 = 100²/100 = 100 Ω
Since, B1 and B2 are connected in parallel.
So, 1/Rp = 1/R1 + 1/R2 = 1/300 + 1/100 = 4/300
⇒ Rp = 300/4 = 75 Ω
So, Req across circuit = 75 + 300 + 25 = 400 Ω
Current that can flow through B1 = V1/R1 = 60/300 = 1/5 A
Current that can flow through B2 = V2/R2 = 100/100 = 1 A
So, maximum current that can flow through the circuit so that all bulbs remain safe = 1/5 A
Therefore, required e.m.f. = IReq = 1/5 x 400 = 80 V - Find equivalent resistance between P and Q:

Sol:
- Find equivalent resistance between P and Q:

Sol:
Here, all resistors are connected in parallel.
So, 1/Rp = 1/R1 + 1/R2 + 1/R3 = 1/10 + 1/10 + 1/10 = 3/10
⇒ Rp = 10/3 Ω - In reference to the given figure, find the current flowing through 20 Ω resistor.

Sol:
RAB = R1 + R2 = 5 + 20 = 25 Ω
RCD = R1 + R2 = 10 + 40 = 50 Ω
1/Req = 1/RAB + 1/RCD = 1/25 + 1/50 = 3/50
⇒ Req = 50/3 Ω
I = 3 A
So, V = IReq = 3 x 50/3 =50 V
In parallel, voltage remains same.
So, current flowing through AB, I = V/RAB = 50/25 = 2 A
In series, current flowing through each resistor remains same.
So, current flowing through 20 Ω resistor = 2 A.


Comments
Shivansh preet
If u want to being motivated in your life,
Watch the video:- https://youtube.com/shorts/WDIs9FBnoB0?feature=share
Hairstyles
I know this if off topic but I’m looking into starting my own weblog and was wondering what all is required to get set up? I’m assuming having a blog like yours would cost a pretty penny? I’m not very web savvy so I’m not 100 sure. Any suggestions or advice would be greatly appreciated. Cheers
Hairstyles
Your house is valueble for me. Thanks!?
manvika
thanks for the video bro…..it helped me soo much