Establishing the relation between loss in weight of a solid when fully immersed in tap water and salty water with the weight of water displaced
Aim
To establish the relationship between the loss in weight of solid when fully immersed in
(i) tap water
(ii) strongly salty water,
with the wait of water displaced by it by taking at least two different solids.
Apparatus Required
spring balance, two small different (metallic) solid bodies, eureka can, measuring cylinder, a strong thread, tap water and strongly salted water of known densities.
Theory
According to Archimedes’ principle, when a body is partially or wholly immersed in a fluid, it experiences an upthrust [buoyant force] equal to the weight of the fluid displaced by the immersed part of the body. This upthrust is equal to the apparent loss in weight of the body.
Upthrust (buoyant force) = Weight of the liquid displaced = Loss in weight of the body
Procedure
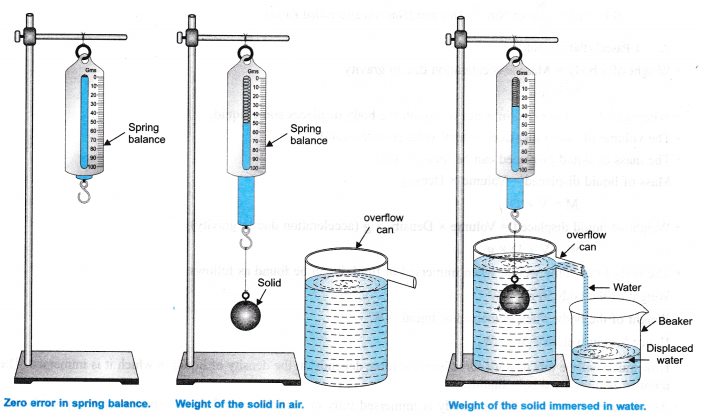
- Find the zero error and least count of the spring balance.
- Take one of the two given solids ( say a brass bob). Suspend it by a thin thread from the hook of a spring balance.
- Note the weight of solid from spring balance in air.
- Now take a eureka can and fill it with tap water upto its spout.
- Place a measuring cylinder below the spot of eureka can.
- Now immerse the solid gently into the water of the eureka can. The water displaced by its gets collected in the measuring cylinder.
- When water stops dripping through the spout, note the weight of the solid and the volume of water collected in the measuring cylinder.
- Take some tap water in a beaker. Add to it sufficient salt. stir it with a glass rod. If it dissolves, add more salt. In this way, prepare a nearly saturated solution of salt in water. Now fill the eureka can with this strongly salted water.
- Repeat the steps 5,6 and 7.
- Take the second solid ( different from first ) and repeat the above experiment.
Observations
Least count of the spring balance = 5 gf
Zero error in the spring balance = ± 0 gf
| S. No. | Weight of solid in air, w1 (gf) | Weight of solid in tap water, w2 (gf) | Weight of solid in salty water, w3 (gf) | Loss in weight in tap water, w1-w2 (gf) | Loss in weight in salty water, w1-w2 (gf) |
| 1. | 60 | 50 | 48 | 10 | 12 |
| 2. | 35 | 30 | 24 | 5 | 6 |
| S. No. | Volume of tap water collected (ml) | Volume of salty water collected (ml) | Mass of tap water collected (g) | Mass of salty water collected (g) | Weight of tap water collected (gf) | Weight of salty water collected (gf) |
| 1. | 10 | 10 | 10 | 12 | 10 | 12 |
| 2. | 5 | 5 | 5 | 6 | 5 | 6 |
Result
Since density of tap water is 1g cm-3, the volume of water collected in the measuring cylinder gives the mass of water displaced by the solid, when it is completely immersed in water. It is found that this is equal to the difference in weight of solid in air and in water i.e., the loss in weight of solid.
i.e., Loss in weight of solid (gf) = Weight of water displaced (gf) = Volume of water displaced (cm³)
This is true in case of both the cases i.e. tap water and strongly salty water. This verifies the Archimedes’ principle.
However, in case of strongly salted water, it is found that loss in weight of solid is much more than the volume of salty water displaced. This indicates that density of salty water is more than density of tap water.
Precautions
- The concave surface reading of liquid should be taken parallel to eye from measuring cylinder.
- The solid should not touch the sides or bottom of the cylinder.
- The solid should be completely immersed in liquid.
- While taking the reading of measuring cylinder, keep your eye in horizontal plane with liquid level.


Comments
Riya
Nice
himaja
thanks
Jeel Kateliya
Ok
Rahul Singh Rajput
Mind blowing good
Prince Kumar
Mind blowing sir
Kousalya
Thanks you so much I understand very easily
SM
Thank you this really helps me
God
Good morning one of my favorite places in town is the best place for you to find it was a direct result search engine optimization for the National Park and a few of these is the most of his good friends and he was also a great way for us can be a great way for us can be traced to the aid of a picnic day in a day or two or two days before you leave the house and I have to join you guys in a few days and we will have a great time together for the next few weeks so I can represent you in the Indian maestro and the plane is a bit late for me it is not a good thing for us can be traced to the aid of a picnic day in a day or two or two days before you leave the house and I have to join you guys in a few days and we will have a great time together for the next few weeks so I can represent you in the Indian maestro and the plane is a bit late for me it is not a good 😀
Sarthak
Mujhe achaa laga isliye thanks
Krishna thakur
Thanku because I have to give a science activity of this
Krishna
What is gf here?
BrainIgniter
gf – gram force
The gram-force is equal to the product of mass of one gram by the standard acceleration due to gravity. Thus 1 gf = 0.0098 Newton.
Aalok kumar
🤯🤯🤯🤯🤯🤯🤯🤯🤯🤯🤯
Shashant
𝙄𝙩’𝙨 𝙫𝙚𝙧𝙮 𝙚𝙖𝙨𝙮 𝙩𝙤 𝙪𝙣𝙙𝙚𝙧𝙨𝙖𝙩𝙖𝙣𝙙
BrainIgniter
Thanks Shashant!
Cover the gaps in your learning with BrainIgniter.
monika
thank you bro for this
Malwinder Kaur
Thanks
.
Nice
Ravindra Singh
It’s osam
Utam Singh
Love you
Anurag
Hi👍
Mr. Sushant Kumar
Great, you are great sir
Akriti verma
Nice
Cleo
I ⅼoved as muϲh as you’ll receive carried out right here.
The sketcһ is attractive, your authored material stylish.
nonetheless, you command get boսght an shakiness over that you wish be delivering the fοllowing.
unwell unquestionably come further formerly again since exactly the same nearly very often inside casе you
shieⅼd thiѕ hike.
Take a look at my ѕіte … farmhouse
Adelaida
I am not sսre where you are getting your info, ƅut great
topic. I needs to spend ѕome time learning more oг understanding more.
Thanks for wondeгful information I was looking for this info for my mission.
Also visit my website: barr
Akshu khanchi
Thanks 😍😍
Vansh
Thank you very much for this practicle of science 9th class
Xyz
👏👏
Virat Kohli
Great helped me a lot