Class 9 Work and Energy Notes
Notes Important QuestionsWork and Energy Notes
Work:-
Work is said to be done if a force is applied on an object & it displaces in the direction of force applied.
- S.I. unit:- Joule (J)
- It is a scalar quantity.
- Work done = Force x displacement (W = FS)
1 Joule :- The work done on an object is said to be 1 joule when a force of 1 N displaces it by 1 m along the line of action of the force.
Positive, Negative and Zero Work Done:-
- W = F S Cos θ

Energy:-
The capacity of doing work is called energy.
- S.I. unit :- Joule (J)
Kinetic energy:-
The energy possessed by an object by virtue of its motion is known as kinetic energy. Ex:- Energy in moving fan.
Expression of kinetic energy:-
Consider an object having mass ‘m’ moving with uniform acceleration ‘a’. Let its initial velocity be ‘u’ & final velocity be ‘v’.
From 2nd law of motion, F = ma
W = FS
or, W = ma(v2-u2)/2a [Since, v2-u2 = 2aS So, S = (v2-u2)/2a]
or, W = m(v2-u2)/2 = ½ m(v2-u2)
If u = 0 then, W = ½ m(v2-02) = ½ mv2
So, Ek = ½ mv2
Work done= Change in kinetic energy
or, W = Ekf -Eki
or, W = ½ mv2 – ½ mu2
Potential energy:-
The energy possessed by an object by virtue of its position or configuration is known as its potential energy. Ex:- Water stored in a dam.
Expression of potential energy:-
Consider an object having mass ‘m’ at a height ‘h’.
From 2nd law of motion,
F = ma = mg (Where, g is acceleration due to gravity.)
Now, W = FS
or, W = mgh [here, S = h]
So, Ep= mgh
Law of conservation of energy:-
It states that energy can neither be created nor be destroyed. It can only be converted from one form to another.
Mechanical energy:-
The sum of kinetic energy & potential energy of an object is known as mechanical energy.
- Mechanical energy = Potential energy +Kinetic energy = constant
Mathematical proof of conservation of mechanical energy for a freely falling object:-
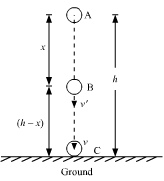
Consider an object having mass ‘m’ at height ‘h’.
At point A, velocity = 0, acceleration = g and height = h
K.E. = ½ mv2 = ½ m.02 = 0
P.E. = mgh
M.E. = K.E.+P.E. = 0 + mgh = mgh
At point B,
Using, v2-u2 = 2aS
or, v2 = 02+2gx [here,u=0, a=g & S=x]
or, v2 = 2gx
K.E.= ½ mv2 = ½ m.2gx = mgx
P.E.= mg(h-x) = mgh – mgx
So, M.E.=K.E.+P.E. = mgx + mgh – mgx = mgh
At point C,
Using, v2-u2 = 2aS
or, v2= u2+2aS = 02+2gh = 2gh
K.E.= ½ mv2 = ½ m(2gh) = mgh
and P.E.= mgh = mg.0 = 0
so, M.E.= K.E.+P.E. = mgh+0 = mgh
Clearly, the total mechanical energy for a freely falling object is ‘mgh’ i.e., constant at every point.
Power:-
The rate of doing work is called power.
- Power= work/time (P=W/t)
- S.I. unit :- J/S or Watt (W)
1 watt of power:- The power of an agent is said to be 1 watt if it does 1 J work in 1 sec.
- 1 kW = 1000 W = 1000 J/s
- Commercial unit of energy :- kilowatt hour (kW h)
Conversion of commercial unit of energy to S.I. unit of energy:-
1 kwh = 1000 W x 3600 sec = 3.6 x106 W sec = 3.6 x106 J
or, 1 unit = 1 kwh = 3.6 x 106 J


Comments
Ayush prabhakar
Its a fabulous website for learning physics
Lead by our class teacher. Suraj sir
BrainIgniter
Thanks a ton Ayush!
Cover the gaps in your learning & enjoy your study with BrainIgniter.