Class 9 Motion Important Questions : Solutions

Important Questions Notes NCERT Solutions

Motion Important Questions : Solution

Define uniform circular motion and give example of it. Why is it called accelerated motion?
Sol:- Uniform circular motion can be described as the motion of an object in a circular path at a constant speed.
Example:- Motion of an electron around the nucleus in a circular orbit, motion of the tip of second’s hand of a watch etc.
Circular motion is always an accelerated motion because the direction of motion changes at every point on the circular path.
A car moves with a speed of 30 km/h for half an hour, 25 km/h for one hour and 40 km/h for two hours. Calculate the average speed of the car.
Sol:- As we know that,
Average speed =
Total distance travelled

Total time taken

Now,
Time = 0.5 + 1 + 2 = 3.5 hr
Distance = (30 x 0.5) + (25 x 1) + (40 x 2) = 15 + 25 + 80 = 120 Km
Hence ,
Average speed = $\inline \dpi{120} \fn_phv \frac{120}{3.5}$ ≈ 34.3 Km/hr
Derive the equation for position – time relation by graphical method.
Sol:-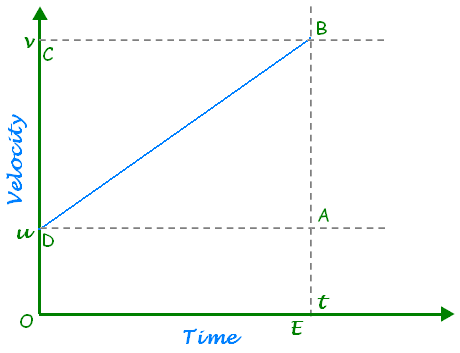

Consider an object moving with initial velocity ‘u’ and uniform acceleration ‘a’. After time ‘t’, let its final velocity becomes ‘v’.
From graph,
OD = u, OC = BE = v, OE = t
Distance travelled = Area of trapezium ODBE
⇒ S = ½ ( sum of parallel sides ) x height
⇒ S = ½ (OD + BE) x OE
⇒ S = ½ (u + v) x t
⇒ S = ½ (u + u + at) x t [∵ v = u + at]
⇒ S = ½ (2u + at) x t
⇒ S = ut + ½ at²
A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s^-2, with what velocity will it strike the ground? After what time will it strike the ground?
Sol:- Given,
u= 0 m/s, g = 10 m/s², h = 20 m
Using, v² – u² = 2aS
⇒ v² – 0² = 2 x 10 x 20
⇒ v² = 400
⇒ v = $\inline \dpi{100} \fn_phv \sqrt{400}$
⇒ v = 20 m/s
Using, v = u + at
⇒ 20 = 0 + 10 x t
⇒ 20 = 10t
⇒ t = 2 sec
Hence, the ball will strike the ground with the velocity of 20 m/s after 2 sec.
A train starts its journey from station P; accelerates at the rate of 2 m s^-2, and reaches its maximum speed in 10 s. It maintains this speed for 30 min and retards uniformly to rest at the station Q after the next 20 s. Calculate:
1. the maximum speed of the train.
2. retardation.
3. the distance between stations P and Q.
  Sol:- (1) Given,
  u = 0 m/s, a = 2 m/s², t = 10 s
  Using, v = u + at
  ⇒ v = 0 + 2 x 10
  ⇒ v = 20 m/s
  (2) Given,
  u = 20 m/s, v = 0 m/s, t = 20 s
  Using, a = $\inline \dpi{150} \frac{v - u}{t}$ = $\inline \dpi{120} \fn_phv \frac{0 -20}{20}$ = -1 m/s²
  (3) S₁ = ut + ½ a t² = 0 x 10 + ½ x 2 x 10² = 100 m
  S₂ = vt = 20 x 30 x 60 = 36000 m
  S₃ = ut + ½ at² = 20 x 20 + ½ x (-1) x 20² = 200 m
  Total distance = S₁ + S₂ + S₃ = 100 + 36000 + 200 = 36300 m = 36.3 km
A boy runs for 20 min at a uniform speed of 18 km/h. At what speed should he run for the next 40 min so that his average speed becomes 24 km/h?
Sol:- Given,
t₁ = 20 min = ⅓ hr and t₂ = 40 min = ⅔ hr
v₁ = 18 km/hr
Average speed = 24 km/hr
Total time = t₁ + t₂ = 20 + 40 = 60 min = 1 hr
Distance covered in 1 hr = Speed x time = 24×1 = 24 km
Distance covered in 20 min (⅓ hr) = v₁ x t₁ = 18 x ⅓ = 6 km
Distance covered in 40 min (⅔ hr) = Distance covered in 1 hr – Distance covered in 20 min (⅓ hr) = 24 – 6 = 18 km
Speed needed for the next 40 min = v₂ = $\frac{distance}{time}$ = $\frac{18}{\frac{2}{3}}$ = 18 x $\frac{3}{2}$ = 27km/hr
Hence, he should run at the speed of 27km/hr for the next 40 min so that his average speed becomes 24 km/h.
A train accelerated from 10 km/h to 40 km/h in 2 minutes. How much distance does it cover in this period? Assume that the tracks are straight.
Sol:-Given,
u = 10 km/hr, v = 40 km/hr, t = 2 min = $\frac{1}{30}$ hr
Using, v = u + at
a = $\inline \dpi{150} \frac{v - u}{t}$ = $\inline \dpi{120} \frac{40 - 10}{\frac{1}{30}}$ = ( 40 – 10 ) x 30 = 900 km/hr²
So, the distance covered = S = ut + 1/2at²
⇒ S = 10 x 1/30 + ½ x 900 x (1/30)²
⇒ S = ⅓ + 450 x 1/900 = ⅓ + ½ = ⅚ km
Hence, distance covered in by the train 2 mins = ⅚ km.
A train starts from rest and accelerates uniformly at the rate of 5 m s^-2 for 5 sec. Calculate the velocity of train in 5 sec.
Sol:- Given,
u = 0 m/s, a = 5 m/s², t = 5 s
Using, v = u + at
⇒ v = 0 + 5 x 5
⇒ v = 25 m/s
Hence, the velocity of train in 5 s is 25 m/s.
A bullet leaves a rifle with a muzzle velocity of 1042 m/s. While accelerating through the barrel of the rifle, the bullet moves a distance of 1.680 m. Determine the acceleration of the bullet (assume a uniform acceleration).
Sol:- Given,
u = 0 m/s, v = 1042 m/s and S = 1.680 m
Using, v² – u² = 2aS
⇒ 1042² – 0² = 2 x a x 1.680
⇒ a = 323144.048 m/s²
Hence, the acceleration of the bullet is 323144.048 m/s².
A bike riding at 22.4 m/s skids to come to a halt in 2.55 s. Find the skidding distance of the bike.
Sol:- Given,
u = 22.4 m/s, v = 0 m/s, t = 2.55 s
Using, v = u + at
⇒ a = $\inline \dpi{150} \frac{v - u}{t}$
⇒ a = $\inline \dpi{120} \frac{0 - 22.4}{2.55}$ ≈ -8.7 m/s²
Now,
Using, S = ut + ½ a t²
⇒ S = 22.4 x 2.55 + ½ x -8.7 x 2.55²
⇒ S = 57.12 + (-28.28) = 28.84 m
Hence, the skidding distance of the bike is 28.84 m.
A race of scooter is seen accelerating uniformly from 18.5 m/s to 46.1 m/s in 2.47 sec. Determine the acceleration of the scooter and the distance traveled.
Sol:- Given,
u = 18.5 m/s, v = 46.1 m/s, t = 2.47 s
Using, a = $\inline \dpi{150} \frac{v - u}{t}$
⇒ a = $\inline \dpi{120} \frac{46.1 - 18.5}{2.47}$ = 27.6 / 2.47 ≈ 11.17 m/s²
Using, 2aS = v² – u²
⇒ 2 x 11.17 x S = 46.1² – 18.5²
⇒ 22.34 x S = 2125.21 – 342.25
⇒ S = 1782.96 / 22.34
⇒ S = 79.81 m
Hence, the acceleration is 11.17 m/s² and distance traveled is 79.81 m
A car is travelling with a speed of 36 km/h. The driver applied the brakes and retards the car uniformly. The car is stopped in 5 sec. Find (i) the acceleration of car and (ii) distance before it stops after applying brakes?
Sol:- Given,
u = 36 Km/h = 36 x 5 / 18 = 10 m/s
v = 0 m/s
t = 5 s
Using, a = $\inline \dpi{150} \frac{v - u}{t}$
⇒ a = $\inline \dpi{150} \frac{0 - 10}{5}$ = -2 m/s²
Using, S = ut + ½ at²
⇒ S = 10 x 5 + ½ x (-2) x 5²
⇒ S = 50 – 25 = 25 m
Hence, (i) The acceleration of car is -2 m/s² and (ii) distance before it stops after applying brakes is 25 m.
Robbers in a car travelling at 20 m/s pass a policeman on a motorcycle at rest. The policeman immediately starts chasing the robbers. The police man accelerates at 3m/s² for 12 s and thereafter travels at a constant velocity. calculate the distance covered by the policeman before he overtakes the car.
Sol:- Let police overtake the robbers in time ‘t’
So, Distance covered by robbers in time ‘t’ = speed x time
= 20t …..(i)
For police
u = 0 m/s, t = 12 s, a = 3 m/s²
Using, v = u + at
⇒ v = 0 + 3 x 12
⇒ v = 36 m/s
Distance covered in 12 s = S = ut + ½ at²
⇒ S = 0 x 12 + ½ x 3 x 12²
⇒ S = 216 m
Let total time taken to overtake be ‘t’ sec.
∴ Remaining time = (t – 12) sec
So, Distance covered = speed x time = 36(t – 12) m
Now,
Distance covered by robbers = Distance covered by police
⇒ 20t = 216 + 36 x (t – 12)
⇒ 20t = 216 + 36t – 432
⇒ 36t – 20t = 432 – 216
⇒ 16t = 216
⇒ t = 13.5 s
So, Distance covered by robbers = 20t = 20 x 13.5 = 270 m
Hence, the distance covered by the policeman before he overtakes the car is 270 m.
The variation of the velocity of a particle moving along a straight line is illustrated in the graph given below. Find the distance covered by the particle in 4 seconds.

Sol:-

Distance covered by the particle in 4 sec
= Area under the graph
= Area of trapezium OABG + Area of trapezium BCFG + Area of rectangle CDEF
= ½ (AB+OG) x AH + ½ (CF+BG) x GF + DE x FE
= ½ (1+2) x 20 + ½ (10+20) x 1 + 10 x 1
= 30 + 15 + 10
= 55 m

Class 9

Class 9 Motion Important Questions : Solutions

Comments

ROHIT

Cancel Reply