Class 10 Electricity Previous Years Questions : Solutions

Electricity Previous Years Questions : Solutions

1. Define 1 kilowatt hour. [1 mark] [CBSE 2019]
   Sol:
   Electrical energy consumed by apliances is said to be 1 kilowatt hour if, it operates power of 1000 watt in 1 hour.
2. The values of mA and µA are: [1 mark] [CBSE 2020]
   1. 10^-6 A and 10^-9 A respectively
   2. 10^-3 A and 10^-6 A respectively
   3. 10^-3 A and 10^-9 A respectively
   4. 10^-6 A and 10^-3 A respectively
      Sol:
      (4.) 10^-6 A and 10^-3 A respectively
3. A cylindrical conductor of length ‘l‘ and uniform area of cross-section ‘A’ has resistance ‘R’. Another conductor of length 2.5 l and resistance 0.5 R of the same material has area of cross-section: [1 mark] [CBSE 2020]
   1. 5 A
   2. 2.5 A
   3. 0.5 A
   4. 1/5 A
      Sol:
      R = ρ^l/_A
      R’ = ρ^l‘/_A’
      or, 0.5R= ρ^2.5l/_A’
      or, 0.5 ρ^l/_A = ρ^2.5l/_A’
      or, A’ = 5 A
      (1.) 5 A
4. Define the term electrical resistivity of a material. [1 mark] [CBSE 2019]
   Sol:
   The resistance of the conductor of unit length & unit area of cross section is called its resistivity.
5. Consider the scale of a voltmeter shown in the diagram and answer the following questions:
   
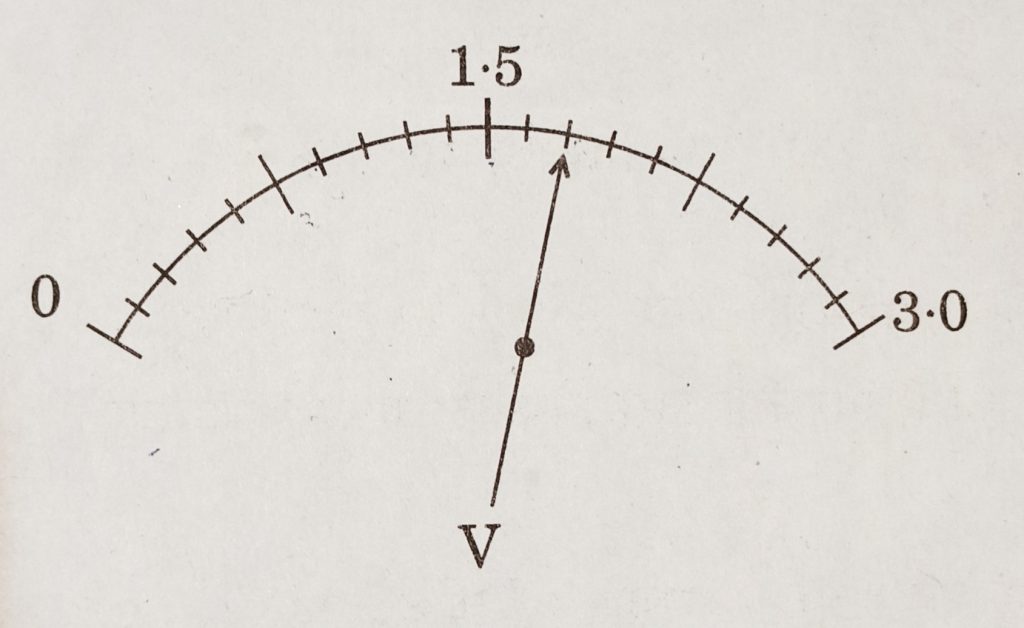
   1. What is the least count of the voltmeter?
   2. What is the reading shown by the voltmeter?
   3. If this voltmeter is connected across a resistor of 20 Ω, how much current is flowing through the resistor? [2 marks] [CBSE 2019]
      Sol:
      1. Least Count = 3 / 20 = 0.15 V
      2. Reading shown by the voltmeter = 1.5 + 0.15 + 0.15 = 1.8 V
      3. V = 1.8 V and R = 20 Ω
      I = V / R
      or, I = 1.8 V / 20 Ω
      or, I = 0.09 A
6. The values of current (I) flowing through a given resistor (R), for the corresponding values of potential difference (V) across the resistor are as given below :

V(volts)	0.5	1.0	1.5	2.0	2.5	3.0	4.0	5.0
I(Amperes)	0.1	0.2	0.3	0.4	0.5	0.6	0.8	1.0

Plot a graph between current (I) and potential difference (V) and determine the resistance (R) of the resistor. [2 marks] [CBSE 2018]
Sol:
From Ohm’s law
R = V /I

7. Show how would you join three resistors each of resistance 9 Ω so that the equivalent resistance of the combination is (i) 13.5 Ω (ii) 6 Ω? [3 marks] [CBSE 2018]
Sol:
(i) To get equivalent resistance of 13.5 Ω, we should connect resistors in following pattern:

1/R_p = 1/9 Ω + 1/9 Ω
or, 1/R_p = 2/9 Ω
or, R_p = 4.5 Ω
R_eq = 9 Ω + 4.5 Ω
or, R_eq = 13.5 Ω

(ii) To get equivalent resistance of 6 Ω, we should connect in following pattern :-
R_s = 9 Ω + 9 Ω
or, R_s = 18 Ω
or, 1/R_eq = 1/18 Ω + 1/ 9 Ω
or, 1/R_eq = 3/18 Ω
or, 1/R_eq = 6 Ω

8. a. Write Joule’s law of heating.
b. Two lamps, one rated 100 W; 220 V, and the other 60 W; 220 V, are connected in parallel to electric mains supply. Find the current drawn by two bulbs from the line, if the supply voltage is 220 V. [3 marks] [CBSE 2018]
Sol:
(a.)According to Joule’s law of heating, heat produced in a resistor is directly proportional to

• square of current (H ∝ I²)
• resistance (H ∝ R)
• time for which current flows (H ∝ t)

H = I²Rt
(b.) Using : P = V² / R
For 1st lamp :
100 = 220² / R₁
or, R₁ = 220² /100 Ω
For 2nd lamp :
60 = 220² / R₂
or, R₂ = 220² / 60 Ω
1/ R_eq = 1/ R₁ + 1/ R₂
or, 1/ R_eq = 100 / 220² Ω + 60 / 220² Ω
or, 1/R_eq = 160 / 220² Ω
or, R_eq = 220² / 160 Ω
From Ohm’s law
V = IR
or, 220 V = I ( 220² / 160 Ω )
or, I = 0.73 A

9. a. List the factors on which the resistance of a conductor in the shape of a wire depends.
b. Why are metals good conductor of electricity whereas glass is a bad conductor of electricity ?Give reason.
c. Why are alloys commonly used in electrical heating devices? Give reason. [CBSE 2018] [3 Marks]
Sol:
(a) Factors on which the resistance of a conductor in the shape of a wire depends are :
(i) Length of the wire (l)
(ii) Cross section area of the wire (A)
Note :- Other physical factors on which the resistance of a wire depends like :- temperature and Nature of the material.
(b) Metals are good conductor of electricity because they have the large number of free ions whereas Glass has no free ions to conduct electricity. So, Glass is a bad conductor of electricity.
(c) Alloys are commonly used in electrical heating devices because :
(i) They have high melting and boiling point.
(ii) They have high resistivity.
(iii) They do not oxidise easily even at high temperature.

10. a. Three resistors of resistances R₁, R₂ & R₃ are connected (i) in series , & (ii) in parallel. Write expressions for the equivalent resistance of the combination in each case.
b. Two identical resistors of 12 Ω each are connected to a battery of 3 V. Calculate the ratio of the power consumed by the resulting combinations with minimum resistance & maximum resistance. [CBSE 2019] [5 Marks]
Sol:
(a) When the resistors are connected in series :
R_eq = R₁ + R₂ + R₃
When the resistors are connected in parallel :
1/R_eq = 1/R₁ + 1/R₂ + 1/R₃
(b) When two resistors are connected in series (maximum resistance)
R_eq = 12 + 12 = 24 Ω
P = V² / R
or, P = 3² / 24
or, P = 3/8 W ……….. (i)
when two resistors are connected in parallel (minimum resistance)
1 / R_eq = 1/12 + 1/12
or, R_eq = 6 Ω
P’ = V² / R
or, P’ = 3² / 6
or, P’ = 3/2 W ……….. (ii)
Now, On comparing (i) and (ii)
P / P’ = ^3/8/_3/2
or, P / P’ = 1 / 4
or, P : P’ = 1 : 4

11. a. Write the relation between resistance & electrical resistivity of the material of a conductor in the shape of a cylinder of length ‘l’ & area of cross section ‘A’ . Hence derive the S.I. unit of electrical resistivity.
b. Resistance of a metal wire of length 5 m is 100 Ω. If the area of cross section of the wire is 3 x 10^-7 m², calculate the resistivity of the metal. [5 Marks] [CBSE 2019]
Sol:
(a) The relation between resistance and electrical resistivity ;
R = ρ ^l/_A
SI unit of resistivity :- ohm meter (Ω m)
Derivation : R = ρ ^l/_A
or, ρ = ^RA/_l
or, ρ = Ω ^m2 /_m
or, ρ = Ω m
(b) l = 5 m
R = 100 Ω
A = 3 x 10^-7 m²
Using ρ = ^RA/_l
or, ρ = 100 x 3 x 10^-7 / 5
or, ρ = 6 x 10 ^–6 Ω m

12. a. Two lamps rated 100 W, 220 V& 10 W , 220 V are connected in parallel to 220 V supply , calculate the total current through the circuit.
b. Two resistors x & y of resistances 2 Ω & 3 Ω respectively are first joined in parallel & then in series . In each case the voltage supplied is 5 V.
(i) Draw circuit diagrams to show the combination of resistors in each case.
(ii) Calculate the voltage across the 3 Ω resistor in the series combination of resistors. [CBSE 2020] [5 Marks]
Sol:
(a) For 1st lamp
P = VI
or, I₁ = ^P₁ / V
or, I₁ = ¹⁰⁰/₂₂₀ A
For 2nd lamp
P = VI
or, I₂ = ^P₂ / V
or, I₂ = ¹⁰/₂₂₀ A
Total current: I = I₁ + I₂
or, I = ¹⁰⁰/₂₂₀ A + ¹⁰/₂₂₀ A
or, I = ¹¹⁰/₂₂₀ A
or, I = 0.5 A
(b)

R₁ = 3 Ω
R₂ = 2 Ω
R_eq = R₁ + R₂
or, R_eq = 2 Ω + 3 Ω
or, R_eq = 5 Ω
V = 5 V
I = ^V / R_eq
or, I = ⁵ / 5
or, I = 1 A
The voltage across the 3 Ω resistor in the series combination of resistors :
V = IR
or, V = 1 A x 3 Ω
or, V = 3 Ω

13. a. State ohm’s law.
b. How is an ammeter connected in an electric circuit?
c. The power of a lamp is 100 W. Find the energy consumed by it in 1 minute.
d. A wire of resistance 5 Ω is bent in the form of a closed circle. Find the resistance between two points at the ends of any diameter of the circle. [5 marks] [CBSE 2020]
Sol:
(a) At constant temperature, the potential difference across the ends of a conductor is directly proportional to the amount of current flowing through it.

Mathematically,
V ∝ I
V = IR where, R is constant of proportionality & is known as resistance.
(b) An ammeter always connected in series in an electric circuit.
(c) P = 100 W
t = 1 min = 60 sec
Using, E = P x t
or, E = 100 W x 60 sec
or, E = 6000 J
(d) The diametrically opposite points divides the resistance into half of the total resistance. 
R₁ = R₂ = 5/2 = 2.5 Ω
Here, In a circle resistance are connected in parallel
¹/_Req = ¹/_R1 + ¹/_R2
or, ¹/_Req = ¹/_2.5 Ω + ¹/2.5 Ω
or, ¹/_Req = 2/_2.5 Ω
or, R_eq = 1.25 Ω