Class 10 Triangles Previous Years Questions

Previous Years Questions Important Questions

Triangles – Previous Years Questions

1. Let △ABC ~ △DEF and their areas be respectively 81 cm² and 144 cm² . If EF = 24 cm, then length of side BC is _________ cm. [CBSE 2020] [1 Mark]
2. Given △ABC ~ △PQR, if AB/PQ = ⅓, then find the (ar △ABC)/(ar △PQR). [CBSE 2018] [1 Mark]
3. The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 9 cm long, find the length of the corresponding side of the second triangle. [CBSE 2020] [2 Marks]
4. In figure, △PQR is right-angled at P. M is a point on QR such that PM is perpendicular to QR. Show that PQ² = QM x QR.
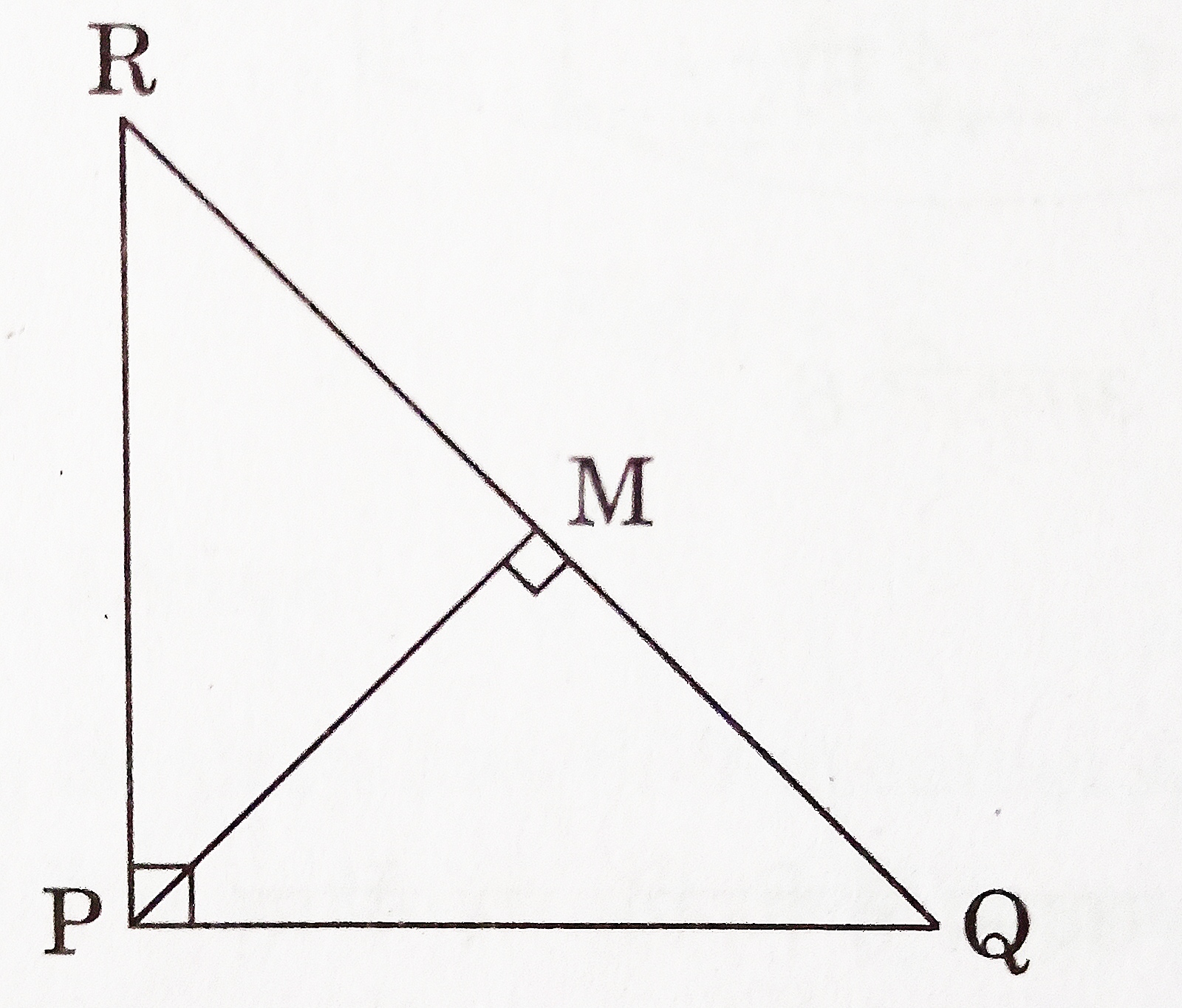   [CBSE 2020] [2 Marks]
5. Prove that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonal. [CBSE 2018] [3 Marks]
6. If the area of two similar triangles are equal, prove that they are congruent. [CBSE 2018] [3 Marks]
7. The perpendicular from A on side BC of a triangle ABC meets BC at D such that DB = 3CD. Prove that 2AB² = 2AC² + BC² . [CBSE 2019] [3 Mark]
8. AD and PM are medians of triangles ABC and PQR respectively where △ABC ~ △PQR. Prove that AB/PQ = AD/PM. [CBSE 2019] [3 Mark]
9. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio. [CBSE 2019] [4 Marks]
10. Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. [CBSE 2019, 2020] [4 Marks]
11. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio. [CBSE 2020] [4 Marks]
12. In a right-angled triangle, prove that the square of the hypotenuse is equal to the sum of the squares of the other two sides. [CBSE 2020] [4 Marks]
13. In an equilateral △ABC, D is a point on side BC such that BD = ⅓ BC. Prove that 9(AD)² = 7(AB)² . [CBSE 2018] [4 Marks]
14. Prove that in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides. [CBSE 2018] [4 Marks]