Class 10 Some Applications of Trigonometry Previous Years Questions
Previous Years Questions Important QuestionsSome Applications of Trigonometry – Previous Years Questions
- A ladder, leaning against a wall, makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder. [CBSE 2016] [1 Mark]
- If the shadow of a vertical pole at a particular time of the day is equal to √ 3 times its height, then what is the elevation of the source of light at that time ? [CBSE 2017] [1 Mark]
- In figure, a tightly stretched rope of length 20 m is tied from the top of a vertical pole to a ground. Find the height of the pole if the angle made by the rope with the ground is 30°.
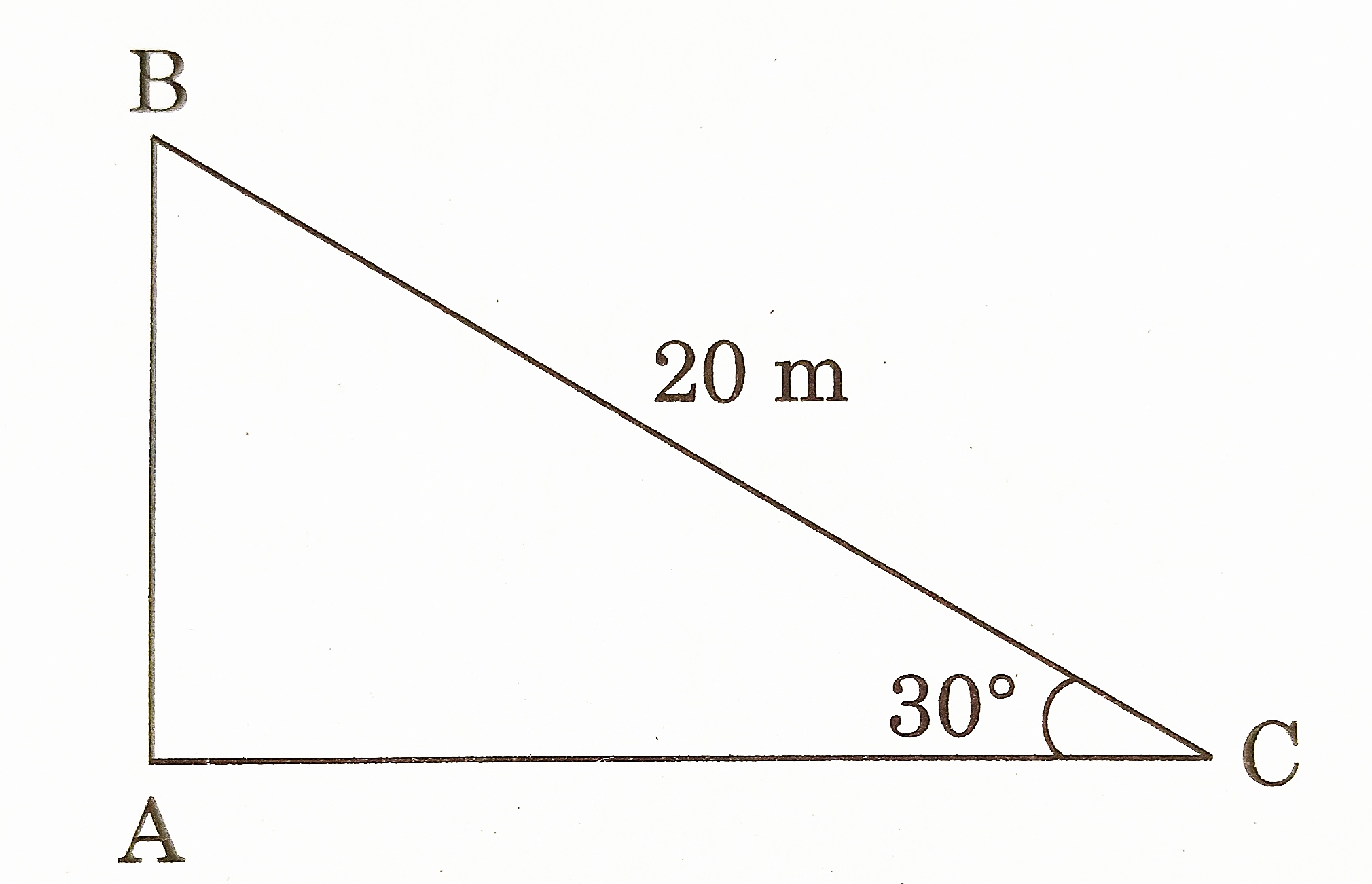 [CBSE 2020] [1 Mark]
[CBSE 2020] [1 Mark] - A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of hill as 30°. Find the distance of the hill from the ship and the height of the hill. [CBSE 2016] [3 Marks]
- A ladder is leaning against a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Find the height of the wall. Also, find the length of the ladder. [CBSE 2017] [3 Marks]
- The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45°. Find the height of the tower PQ and the distance PX. (Use √ 3 = 1.73) [CBSE 2016] [4 Marks]
- A 2 m tall boy is standing at some distance from a 29 m tall building. The angle of elevation, from his eyes to the top of the building increases from 30° to 60°, as he walks towards the building. Find the distance he walked towards the building. [CBSE 2017] [4 Marks]
- As observed from the top of a 100 m high light house from the sea-level , the angles of depression of two ships are 30° and 45°. If one ship exactly behind the other on the same side of the light house, find the distance between the two ships. (Use √ 3 = 1.732) [CBSE 2018] [4 Marks]
- The shadow of a tower standing on a level ground is found to be 40 m longer when the sun’s altitude is 30° than when it was 60°. Find the height of the tower. (Given √ 3 = 1.732) [CBSE 2019] [4 Marks]
- A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30° , which is approaching the foot of the tower with a uniform speed. After covering a distance of 50 m, the angle of depression of the car becomes 60°. Find the height of the tower. ( Use √ 3 = = 1.73) [CBSE 2020] [4 Marks]
- From the top of a 7 m building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Use √ 3 = 1.73) [CBSE 2020] [4 Marks]


Comments