Class 10

Class 10 – Introduction to Trigonometry – Previous years Questions

Previous Years Questions Important Questions

Introduction to Trigonometry – Previous years Questions

  1. The value of θ for which cos(10° + θ) = sin 30° , is
    1. 50°
    2. 40°
    3. 80°
    4. 20° [CBSE 2020] [1 Mark]
  2. The value of θ for which sin (44° + θ) = cos 30° , is
    1. 46°
    2. 60°
    3. 16°
    4. 90° [CBSE 2020] [1 Mark]
  3. If tan A = 1, then 2 sin A cos A = ________. [CBSE 2020] [1 Mark]
  4. What is the value of (cos2 67° – sin2 23°)? [CBSE 2018] [1 Mark]
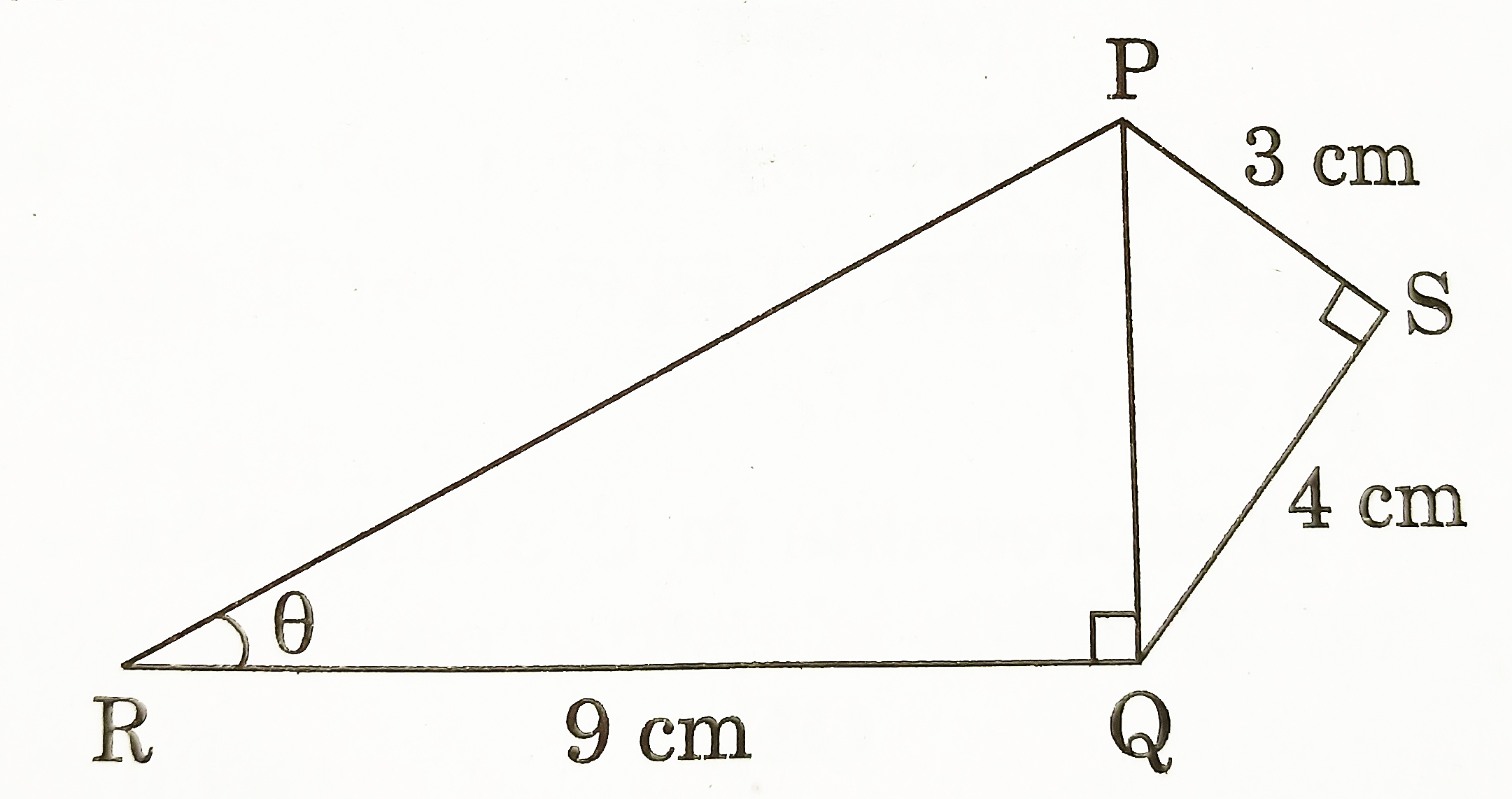
  5. In figure, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90° , PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ. [CBSE 2019] [1 Mark]
  6. If tan α = 5/12, find the value of sec α. [CBSE 2019] [1 Mark]
  7. Evaluate:
    \left ( \frac{sin 47^{\circ}}{cos 43^{\circ}} \right )^{2} + \left ( \frac{cos 30^{\circ}}{cot 30^{\circ}} \right )^{2} - \left ( sin 60^{\circ} \right )^{2} [CBSE 2020] [2 Marks]
  8. Evaluate:
    \frac{2 sin 68^{\circ}}{cos 22^{\circ}} - \frac{2 cot 15^{\circ}}{tan 75^{\circ}} - 3 tan 40^{\circ} tan 45^{\circ} tan 50^{\circ} [CBSE 2020] [2 Marks]
  9. If 4 tan θ = 3, evaluate
    \frac{4 sin \theta - cos \theta + 1}{4 sin \theta + cos \theta - 1}. [CBSE 2018] [3 Marks]
  10. If tan 2A = cot(A -18°), where 2A is an acute angle, find the value of A. [CBSE 2018] [3 Marks]
  11. A, B and C are interior angles of a triangle ABC. Show that
    1. sin \frac{B + C}{2} = cos \frac{A}{2}
    2. If ∠A = 90°, then find the value of tan\frac{B + C}{2}. [CBSE 2019] [3 Marks]
  12. If tan (A+B) = 1 and tan (A-B) = 1/√3, 0° < A+B < 90°, A>B, then find the value of A and B. [CBSE 2019] [3 Marks]
  13. Prove that :
    \frac{sin \theta - cos \theta + 1}{cos \theta + sin \theta -1} = \frac{1}{sec \theta - tan \theta } [CBSE 2020] [3 Marks]
  14. Prove that
    \frac{sin A - 2 sin^{3}A}{2 cos^{3}A - cos A} = tan A. [CBSE 2018] [4 Marks]
  15. If 1+sin2 θ = 3sin θ cos θ, then prove that tan θ = 1 or tan θ = 1/2. [CBSE 2019] [4 Marks]
  16. Prove the following:
    \frac{1}{1 + sin^{2}\theta } + \frac{1}{1 + cos^{2}\theta } + \frac{1}{1 + sec^{2}\theta } + \frac{1}{1 + cosec^{2}\theta } = 2 [CBSE 2019] [4 Marks]
  17. Prove that:
    \frac{tan^{3}\theta }{1 + tan^{2}\theta } + \frac{cot^{3}\theta }{1 + cot^{2}\theta } = sec \theta cosec \theta - 2 sin \theta cos \theta [CBSE 2019] [4 Marks]

Comments

The maximum upload file size: 100 MB. You can upload: image. Drop file here