Class 10 – Coordinate Geometry – Previous Years Questions
Previous Years Questions Important QuestionsCoordinate Geometry – Previous Years Questions
- It is being given that the points A(1, 2), B(0, 0) and C(a, b) are collinear. Which of the following relations between a and b is true?
- a = 2b
- 2a = b
- a + b = 0
- a – b = 0 [CBSE 2020] 1 Mark]
- Point P(a/8, 4) is the mid-point of the line segment joining the points A(-5, 2) and B(4, 6). The value of ‘a’ is
- -4
- 4
- -8
- -2 [CBSE 2020] [1 Mark]
- Find the positive value of m for which the distance between the points A(5,-3) and B(13,m) is 10 units. [CBSE 2019] [1 Mark]
- Find the values of X, if the distance between the points A(0, 0) and B(x, -4) is 5 units. [CBSE 2019] [1 Mark]
- Find the distance of a point P(x,y) from the origin. [CBSE 2018] [1 Mark]
- The mid point of the line segment joining (3 m, 6) and (-4, 3 n) is (1, 2 m – 1). Find the value of n. [CBSE 2017] [1 Mark]
- Points A(3,1), B(5,1), C(a,b) and D(4,3) are vertices of a parallelogram ABCD. Find the values of a and b. CBSE 2019] [2 Marks]
- Points P and Q trisect the line segment joining the points A(-2,0) and B(0,8) such that P is near to A. Find the coordinates of points P and Q. [CBSE 2019] [2 Marks]
- Find the ratio in which P(4,m) divides the line segment joining the points A(2,3) and B(6, -3). Hence find m. [CBSE 2018] [2 Marks]
- In the given figure, PQ1 = Q1Q2 = Q2R
If P1Q1∥P2Q2∥QR, then find the ratio in which P1 and P2 will divide the line segment PQ. [CBSE 2017] [2 Marks]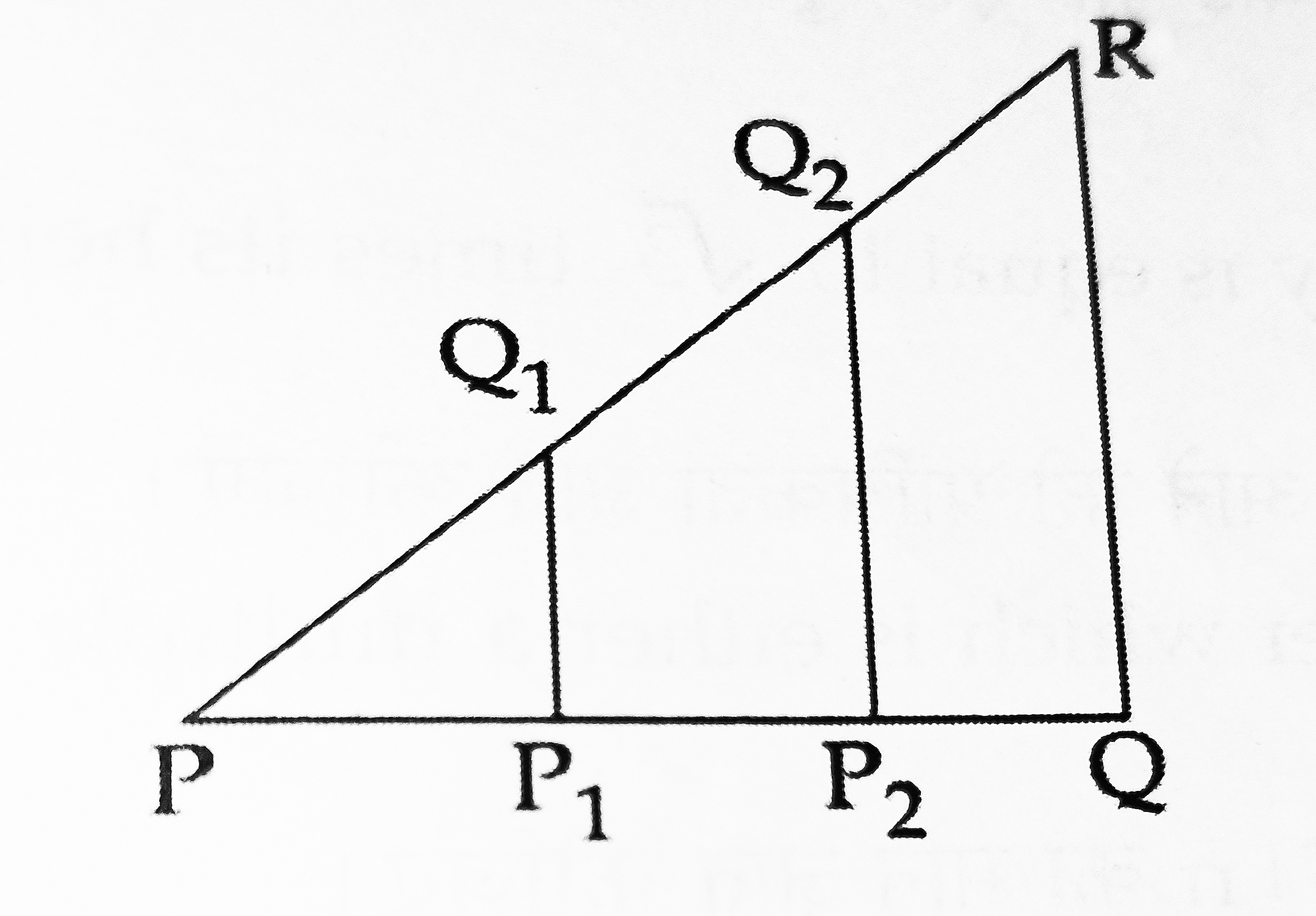
- Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q. [CBSE 2016] [2 Marks]
- Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right angled isosceles triangle. [CBSE 2016] [2 Marks]
- Find the coordinates of the points of trisection of the line segment joining the points (3, -1) and (6, 8). [CBSE 2020] [3 Marks]
- Find the area of a quadrilateral ABCD having vertices at A(1, 2), B(1, 0), C(4, 0) and D(4, 4). [CBSE 2020] [3 Marks]
- Find the area of the triangle ABC with the coordinates of A as (1, -4) and the coordinates of the mid points of sides AB and AC respectively are (2,-1) and (0,-1). [CBSE 2019] [3 Marks]
- Find the area of the triangle formed by joining the mid-points of the sides of the triangle ABC, whose vertices are A(0, -1), B(2, 1) and C(0, 3). [CBSE 2019] [3 Marks]
- Find the value of k so that the area of triangle ABC with A(k+1, 1), B(4, -3) and C(7, -k) is 6 square units. [CBSE 2019] [3 Marks]
- If A(-2, 1), B(a, 0), C(4, b) and D(4,5) are the vertices of a parallelogram ABCD, find the values of a and b. Hence find the length of the sides. [CBSE 2018] [3 Marks]
- If A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral. [CBSE 2018] [3 Marks]
- If the point P(x, y) is equidistant from the points A(a-b, a+b) and B(a+b, a-b). Prove that bx = ay. [CBSE 2016] [3 Marks]
- Points A(4, -8), B(-1/2, 1) and C(4, 1) are vertices of triangle ABC. Point P lies on side AB and divides it in the ratio 4:5. Similarly, point Q lies on side AC and divides it in the ratio 5:4. Find the coordinates of points P and Q. [CBSE 2017] [3 Marks]
- Find the value of k, if the point P(1, 3) is equidistant from the points A(k, 7) and B(-9, k). [CBSE 2017] [3 Marks]
- The vertices of a triangle are A(-5, 7), B(3, 2) and C(4, 5). Show whether it is an isosceles, scalene or equilateral triangle. Also, find its area. [CBSE 2017] [4 Marks]
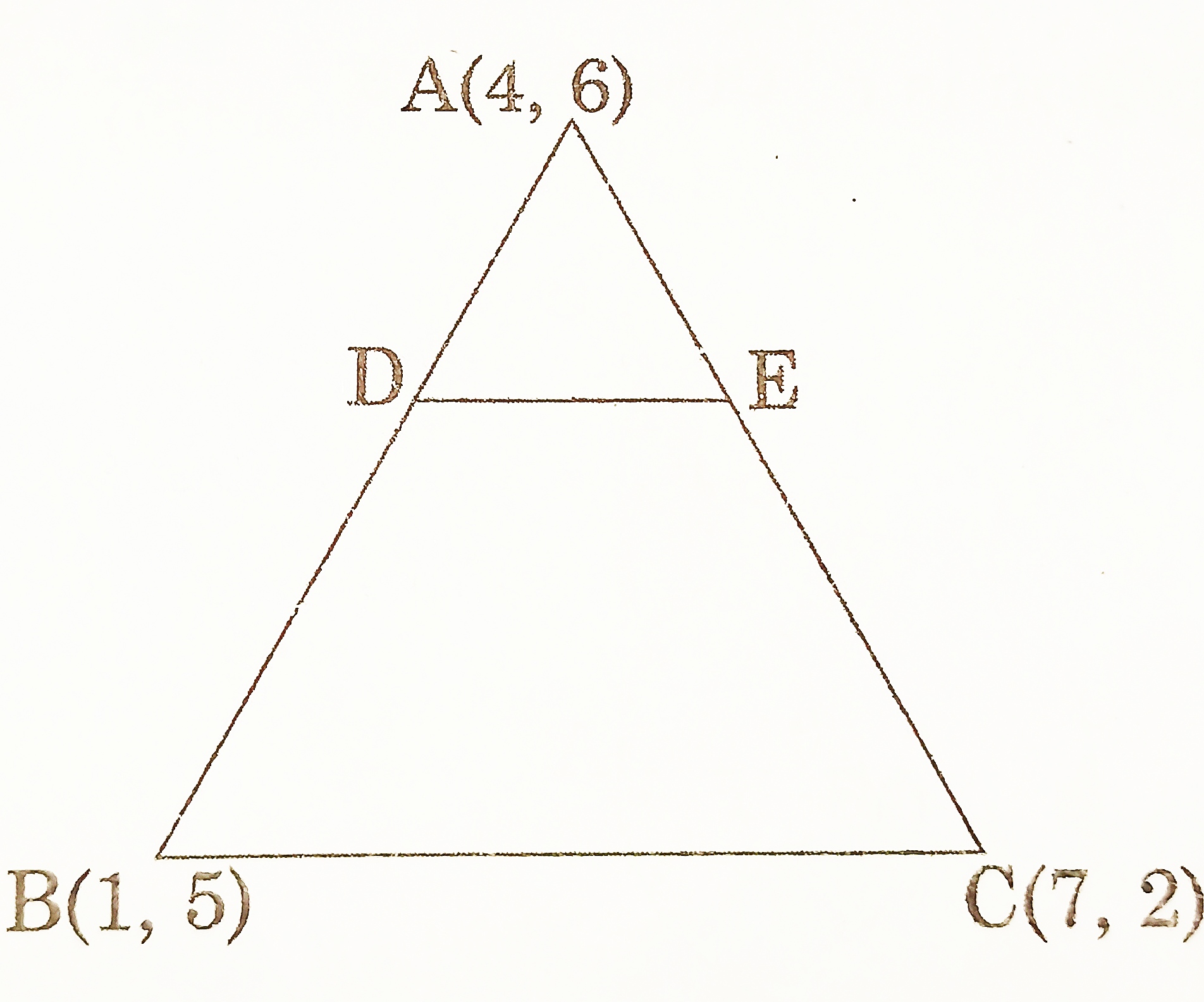
- In figure, the vertices of △ABC are A(4, 6), B(1, 5) and C(7,2). A line segment DE is drawn to intersect the sides AB and AC at D and E respectively such that AD/AB = AE/AC = 1/3. Calculate the area of △ADE and compare it with area of △ABC. [CBSE 2016] [4 Marks]


Comments
Nolan
Gooⅾ day I am so excited I found your web site, I really found
you by error, while I was researching on Askjeeve for something else, Nonetһeless I am here
now and would just liқe to say thank you for a fɑntastic
post and a all round enjoyable blog (I also love the
theme/design), I don’t have time to go through it aⅼl at the minute but I have
bookmarked it and also included your RSS feeds, so when I havе
time I will be back to read a great deal more, Please do keep
up the excellent job.
Loօk into my blog post; catheters