Class 9 Motion Important Questions : Solutions
Important Questions Notes NCERT SolutionsMotion Important Questions : Solution
- Define uniform circular motion and give example of it. Why is it called accelerated motion?
Sol:- Uniform circular motion can be described as the motion of an object in a circular path at a constant speed.
Example:- Motion of an electron around the nucleus in a circular orbit, motion of the tip of second’s hand of a watch etc.
Circular motion is always an accelerated motion because the direction of motion changes at every point on the circular path. - A car moves with a speed of 30 km/h for half an hour, 25 km/h for one hour and 40 km/h for two hours. Calculate the average speed of the car.
Sol:- As we know that,
Average speed =Total distance travelledTotal time taken
Now,
Time = 0.5 + 1 + 2 = 3.5 hr
Distance = (30 x 0.5) + (25 x 1) + (40 x 2) = 15 + 25 + 80 = 120 Km
Hence ,
Average speed =≈ 34.3 Km/hr
- Derive the equation for position – time relation by graphical method.
Sol:-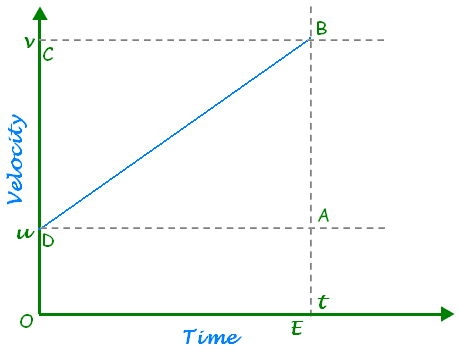
Consider an object moving with initial velocity ‘u’ and uniform acceleration ‘a’. After time ‘t’, let its final velocity becomes ‘v’.
From graph,
OD = u, OC = BE = v, OE = t
Distance travelled = Area of trapezium ODBE
⇒ S = ½ ( sum of parallel sides ) x height
⇒ S = ½ (OD + BE) x OE
⇒ S = ½ (u + v) x t
⇒ S = ½ (u + u + at) x t [∵ v = u + at]
⇒ S = ½ (2u + at) x t
⇒ S = ut + ½ at2 - A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s-2, with what velocity will it strike the ground? After what time will it strike the ground?
Sol:- Given,
u= 0 m/s, g = 10 m/s2, h = 20 m
Using, v2 – u2 = 2aS
⇒ v2 – 02 = 2 x 10 x 20
⇒ v2 = 400
⇒ v =
⇒ v = 20 m/s
Using, v = u + at
⇒ 20 = 0 + 10 x t
⇒ 20 = 10t
⇒ t = 2 sec
Hence, the ball will strike the ground with the velocity of 20 m/s after 2 sec. - A train starts its journey from station P; accelerates at the rate of 2 m s-2, and reaches its maximum speed in 10 s. It maintains this speed for 30 min and retards uniformly to rest at the station Q after the next 20 s. Calculate:
- the maximum speed of the train.
- retardation.
- the distance between stations P and Q.
Sol:- (1) Given,
u = 0 m/s, a = 2 m/s2, t = 10 s
Using, v = u + at
⇒ v = 0 + 2 x 10
⇒ v = 20 m/s
(2) Given,
u = 20 m/s, v = 0 m/s, t = 20 s
Using, a ==
= -1 m/s2
(3) S1 = ut + ½ a t2 = 0 x 10 + ½ x 2 x 102 = 100 m
S2 = vt = 20 x 30 x 60 = 36000 m
S3 = ut + ½ at2 = 20 x 20 + ½ x (-1) x 202 = 200 m
Total distance = S1 + S2 + S3 = 100 + 36000 + 200 = 36300 m = 36.3 km
- A boy runs for 20 min at a uniform speed of 18 km/h. At what speed should he run for the next 40 min so that his average speed becomes 24 km/h?
Sol:- Given,
t1 = 20 min = ⅓ hr and t2 = 40 min = ⅔ hr
v1 = 18 km/hr
Average speed = 24 km/hr
Total time = t1 + t2 = 20 + 40 = 60 min = 1 hr
Distance covered in 1 hr = Speed x time = 24×1 = 24 km
Distance covered in 20 min (⅓ hr) = v1 x t1 = 18 x ⅓ = 6 km
Distance covered in 40 min (⅔ hr) = Distance covered in 1 hr – Distance covered in 20 min (⅓ hr) = 24 – 6 = 18 km
Speed needed for the next 40 min = v2 ==
= 18 x
= 27km/hr
Hence, he should run at the speed of 27km/hr for the next 40 min so that his average speed becomes 24 km/h. - A train accelerated from 10 km/h to 40 km/h in 2 minutes. How much distance does it cover in this period? Assume that the tracks are straight.
Sol:-Given,
u = 10 km/hr, v = 40 km/hr, t = 2 min =hr
Using, v = u + at
a ==
= ( 40 – 10 ) x 30 = 900 km/hr2
So, the distance covered = S = ut + 1/2at2
⇒ S = 10 x 1/30 + ½ x 900 x (1/30)2
⇒ S = ⅓ + 450 x 1/900 = ⅓ + ½ = ⅚ km
Hence, distance covered in by the train 2 mins = ⅚ km. - A train starts from rest and accelerates uniformly at the rate of 5 m s-2 for 5 sec. Calculate the velocity of train in 5 sec.
Sol:- Given,
u = 0 m/s, a = 5 m/s2, t = 5 s
Using, v = u + at
⇒ v = 0 + 5 x 5
⇒ v = 25 m/s
Hence, the velocity of train in 5 s is 25 m/s. - A bullet leaves a rifle with a muzzle velocity of 1042 m/s. While accelerating through the barrel of the rifle, the bullet moves a distance of 1.680 m. Determine the acceleration of the bullet (assume a uniform acceleration).
Sol:- Given,
u = 0 m/s, v = 1042 m/s and S = 1.680 m
Using, v2 – u2 = 2aS
⇒ 10422 – 02 = 2 x a x 1.680
⇒ a = 323144.048 m/s2
Hence, the acceleration of the bullet is 323144.048 m/s2. - A bike riding at 22.4 m/s skids to come to a halt in 2.55 s. Find the skidding distance of the bike.
Sol:- Given,
u = 22.4 m/s, v = 0 m/s, t = 2.55 s
Using, v = u + at
⇒ a =
⇒ a =≈ -8.7 m/s2
Now,
Using, S = ut + ½ a t2
⇒ S = 22.4 x 2.55 + ½ x -8.7 x 2.552
⇒ S = 57.12 + (-28.28) = 28.84 m
Hence, the skidding distance of the bike is 28.84 m. - A race of scooter is seen accelerating uniformly from 18.5 m/s to 46.1 m/s in 2.47 sec. Determine the acceleration of the scooter and the distance traveled.
Sol:- Given,
u = 18.5 m/s, v = 46.1 m/s, t = 2.47 s
Using, a =
⇒ a == 27.6 / 2.47 ≈ 11.17 m/s2
Using, 2aS = v2 – u2
⇒ 2 x 11.17 x S = 46.12 – 18.52
⇒ 22.34 x S = 2125.21 – 342.25
⇒ S = 1782.96 / 22.34
⇒ S = 79.81 m
Hence, the acceleration is 11.17 m/s2 and distance traveled is 79.81 m - A car is travelling with a speed of 36 km/h. The driver applied the brakes and retards the car uniformly. The car is stopped in 5 sec. Find (i) the acceleration of car and (ii) distance before it stops after applying brakes?
Sol:- Given,
u = 36 Km/h = 36 x 5 / 18 = 10 m/s
v = 0 m/s
t = 5 s
Using, a =
⇒ a == -2 m/s2
Using, S = ut + ½ at2
⇒ S = 10 x 5 + ½ x (-2) x 52
⇒ S = 50 – 25 = 25 m
Hence, (i) The acceleration of car is -2 m/s2 and (ii) distance before it stops after applying brakes is 25 m. - Robbers in a car travelling at 20 m/s pass a policeman on a motorcycle at rest. The policeman immediately starts chasing the robbers. The police man accelerates at 3m/s2 for 12 s and thereafter travels at a constant velocity. calculate the distance covered by the policeman before he overtakes the car.
Sol:- Let police overtake the robbers in time ‘t’
So, Distance covered by robbers in time ‘t’ = speed x time
= 20t …..(i)
For police
u = 0 m/s, t = 12 s, a = 3 m/s2
Using, v = u + at
⇒ v = 0 + 3 x 12
⇒ v = 36 m/s
Distance covered in 12 s = S = ut + ½ at2
⇒ S = 0 x 12 + ½ x 3 x 122
⇒ S = 216 m
Let total time taken to overtake be ‘t’ sec.
∴ Remaining time = (t – 12) sec
So, Distance covered = speed x time = 36(t – 12) m
Now,
Distance covered by robbers = Distance covered by police
⇒ 20t = 216 + 36 x (t – 12)
⇒ 20t = 216 + 36t – 432
⇒ 36t – 20t = 432 – 216
⇒ 16t = 216
⇒ t = 13.5 s
So, Distance covered by robbers = 20t = 20 x 13.5 = 270 m
Hence, the distance covered by the policeman before he overtakes the car is 270 m. - The variation of the velocity of a particle moving along a straight line is illustrated in the graph given below. Find the distance covered by the particle in 4 seconds.

Sol:-
Distance covered by the particle in 4 sec
= Area under the graph
= Area of trapezium OABG + Area of trapezium BCFG + Area of rectangle CDEF
= ½ (AB+OG) x AH + ½ (CF+BG) x GF + DE x FE
= ½ (1+2) x 20 + ½ (10+20) x 1 + 10 x 1
= 30 + 15 + 10
= 55 m


Comments
ROHIT
GOOD