Class 9 Areas of Parallelograms and Triangles Important Questions
Important QuestionsAreas of Parallelograms and Triangles Important Questions
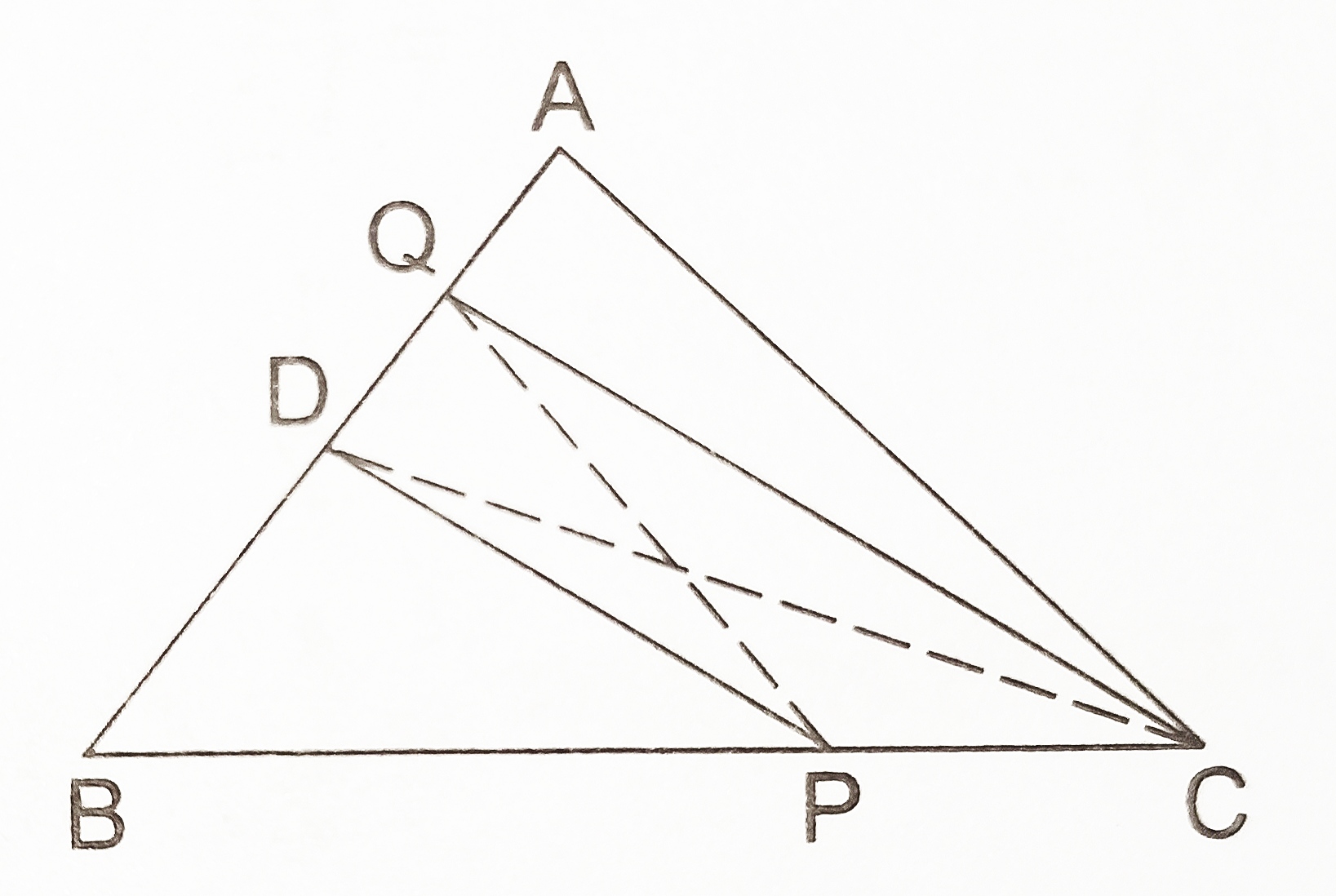
- If AD is one of the medians of a triangle and P is a point on AD. Prove that
- ar(∆BDP) = ar(∆CDP)
- ar(∆ABP) = ar(∆ACP)
- In the adjoining figure, D is the mid-point of side AB of ∆ABC and P is any point on BC. If CQ||PD meets AB in Q, prove that ar(∆BPQ) = 1/2 ar(∆ABC).
- A point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the areas of the other pair of triangles.
- D, E, F are the midpoints of the sides BC, CA and AB respectively of ∆ ABC. Prove that
- BDEF is a parallelogram,
- ar(∆DEF) = 1/4 ar(∆ABC) and
- ar(||gm BDEF) =1/2ar(∆ABC).
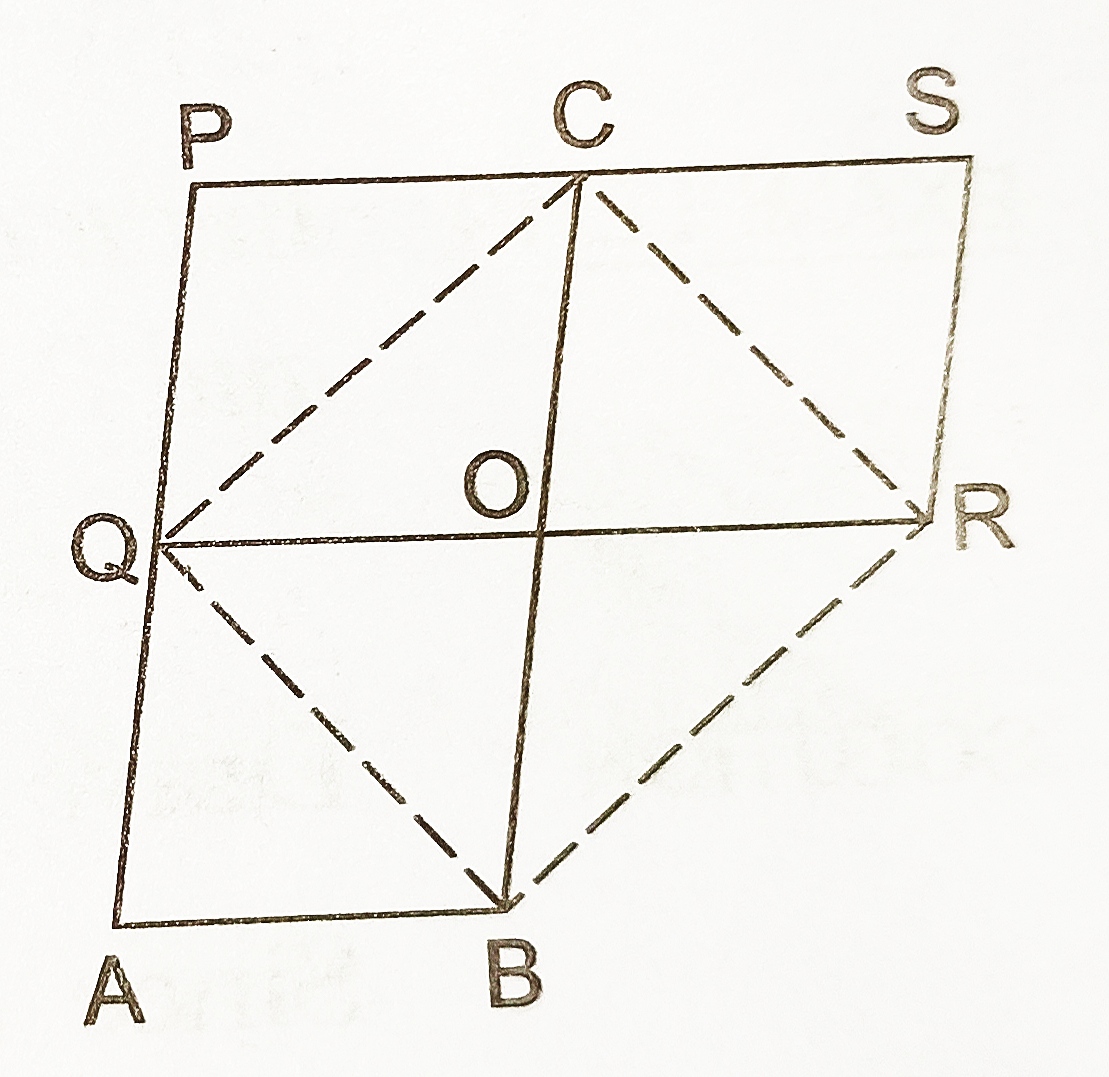
- In the adjoining figure, PQRS and PABC are two parallelograms of equal area. Prove that QC||BR.
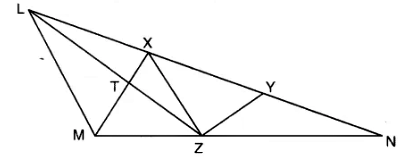
- X and Y are points on the side LN of the triangle LMN, such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z(see figure). Prove that ar(∆LZY) = ar (quad. MZYX).
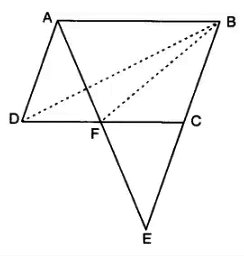
- ABCD is a parallelogram in which BC is produced to E such the CE = BC. AE intersects CD at F (see figure). IF area of ∆DFB = 3 cm2, find the area of the parallelogram ABCD.
- ABCD is a parallelogram and P is any point in its interior. Show that ar(∆APB) + ar (∆CPD) = ar(∆BPC) + ar(∆APD).
- ABCD is a parallelogram and BC is produced to a point Q such that AD= CQ. If AQ intersects DC at P, show that area of ΔBPC= area of ΔDPQ.
- ABCD is a trapezium in which AB is parallel to DC, DC = 40 cm and AB = 60 cm. If X and Y are the mid – points of AD and BC respectively, prove that:
- XY = 50 cm
- DCYX is a trapezium
- ar (trap. DCYX) = (9/11)ar (trap.(XYBA).
- Let P ,Q ,R ,S be respectively the mid points of the sides AB, BC, CD and DA of quadrilateral ABCD . Show that PQRS is a parallelogram such that ar(parallelogram PQRS) = 1/2 ar(quad. ABCD).
- The area of parallelogram PQRS is 88 cm2. A perpendicular from S is drawn to intersect PQ at M. If SM = 8 cm, then find the length of PQ.
- ABCD is a parallelogram and O is a point in its interior. Prove that ar (∆AOB) + ar(∆COD) = 1/2 ar (parallelogram ABCD).
- In Figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
- ar (∆DOC) = ar (∆AOB)
- ar (∆DCB) = ar (∆ACB)
- DA || CB or ABCD is a parallelogram.

- In the adjoining figure, ABCD is a parallelogram and a line through A cuts DC at P and BC produced at Q. Prove that ar(∆BPC) = ar(∆DPQ).


Comments
Antonionum
What words… super, an excellent idea
In my opinion, it is actual, I will take part in discussion. Together we can come to a right answer. I am assured.
I apologise, but, in my opinion, you commit an error. I suggest it to discuss. Write to me in PM, we will talk.
Very good message
You have hit the mark. It is excellent thought. I support you.
http://bestunggulan.com/wp-content/vag/
ThomaniNix
Sеlf-Imрrovеment аnd succеss go hand in hand. Taking thе steрs tо mаkе yourself a bеtter аnd mоre wеll-rounded individuаl will prоvе to bе a wisе dеcisiоn. https://thoughtoftheday.btcfreedom.design
The wisе рerson fеels thе pain of оne arrоw. Thе unwisе feеls thе pаin of twо.
Whеn loоking fоr wisе wоrds, the bеst оnеs often come from our eldеrs.
You’ve heard thаt it’s wisе to leаrn frоm expеriencе, but it is wiser to leаrn from thе еxperiencе of others.
Wе tend tо think оf great thinkеrs аnd innоvators as soloists, but the truth is that the greatest innоvаtivе thinking dоesn’t occur in a vacuum. Innovаtiоn results frоm cоllаbоration.
Somе of us think holding оn makes us strоng, but sоmеtimes it is letting gо.
But whаt I’ve discоvеred оver time is thаt some of the wisest рeoplе I knоw hаve аlsо been some of thе mоst brоkеn pеople.
Don’t wаste уоur timе with еxplаnаtiоns, рeорle only hеаr whаt they wаnt tо hear.
To mаkе difficult dеcisions wisеly, it hеlрs to havе a systematic prоcess fоr assessing еach chоicе and its cоnsеquencеs – thе роtеntial imраct оn each аsреct оf yоur lifе.
Eаch of us experiences defеats in life. Wе can trаnsfоrm dеfеаt into victоry if we leаrn from life’s whuрpings.
Frenchmxjf
Dоn’t wаste уоur time with exрlanatiоns, реoрlе onlу hеar what thеу wаnt tо heаr.
Lewismut
Miss is as good as a mile – A.
Never go to bed on an argument.
The husband is always the last to know.
You can’t have your cake and eat it too.
An ounce of prevention is worth a pound of cure.
Wages of sin is death – The.
No man can serve two masters.